Μικροσεισμοί στον πυθμένα της θάλασσας λόγω συντονισμού κυμάτων στην επιφάνεια

Του Παύλου Χριστοδουλίδη, Επίκουρου Καθηγητή Τεχνολογικού Πανεπιστημίου Κύπρου.

Μικροσεισμοί στον πυθμένα της θάλασσας λόγω συντονισμού / αλληλεπίδρασης κυμάτων στην επιφάνεια

Ο όρος μικροσεισμός συχνά χρησιμοποιείται για να υποδηλώσει τις συνεχείς ταλαντώσεις του εδάφους με περιόδους μεταξύ 3–10 s, που καταγράφονται από ευαίσθητους σεισμογράφους, όχι λόγω των σεισμών ή τοπικών αιτίων όπως βροχές ή ριπές ανέμου. Αυξημένη μικροσεισμική δραστηριότητα μπορεί να παρατηρηθεί ταυτοχρόνως σε μεγάλες περιοχές της Ευρώπης ή της Βόρειας Αμερικής, με τη μεγαλύτερη διαταραχή να συμβαίνει σε παράκτιες περιοχές που συνορεύουν με καλά ανεπτυγμένα κοιλώματα. Είναι πέραν πάσης αμφιβολίας από τη δεκαετία του 1940 ότι οι μικροσεισμοί λαμβάνονται από την κατεύθυνση κοιλωμάτων και μέσα από αυτό το γεγονός έχει αναπτυχθεί μια μέθοδος που αποτελεί τη βάση ενός επιτυχημένου σχεδίου για την παρακολούθηση των τυφώνων στην περιοχή της Καραϊβικής.

Μικροσεισμοί στον ωκεανό μπορούν να ιδωθούν ως κύματα συμπίεσης επαρκούς πλάτους στον βυθό και συμβαίνουν στη ζώνη συχνοτήτων μεταξύ 0,05–1 Hz. Έχουν παρατηρηθεί και σε ρηχά νερά και σε βαθιά νερά. Παράγονται από την αλληλεπίδραση επιφανειακών κυμάτων βαρύτητας (που μπορεί να δημιουργήσουν στάσιμα κύματα) και καταγράφονται ως ‘θόρυβος’ σε σεισμολογικούς σταθμούς σε όλο τον κόσμο. Οι πιο αργοί θόρυβοι στον ωκεανό είναι τα λεγόμενα κύματα ακουστικής-βαρύτητας για βάθος λιγότερο από περίπου το ένα δέκατο του ακουστικού μήκους κύματος. Αυτά τα κύματα ακουστικής-βαρύτητας δεν μπορούν να υπάρξουν στην απουσία επιφανειακών κυμάτων βαρύτητας, κι έτσι περιορίζονται στην περιοχή του ενεργού κυματικού εξαναγκασμού. Να σημειωθεί ότι παρά την ορολογία κύμα ακουστικής-βαρύτητας, η συμπιεστότητα δεν αποτελεί τον βασικό κινητήριο μηχανισμό και τα κύματα ακουστικής-βαρύτητας αφορούν σε απλά κύματα βαρύτητας που έχουν τροποποιηθεί ελαφρώς από επιδράσεις συμπίεσης.

Υπάρχουν δυο τύποι μικροσεισμών, οι πρωτοβάθμιοι και οι δευτεροβάθμιοι. Οι πρωτοβάθμιοι μικροσεισμοί (που δεν αποτελούν αντικείμενο του παρόντος σημειώματος) δημιουργούνται από επιφανειακά κύματα βαρύτητας προσπίπτοντα επί επικλινούς πυθμένα σε ρηχά νερά και έχουν την ίδια περίοδο με τα αιτιώδη κύματα. Οι δε δευτεροβάθμιοι μικροσεισμοί προκύπτουν από τη μη γραμμική αλληλεπίδραση ενός ζεύγους επιφανειακών κυμάτων βαρύτητας με συχνότητες f και f ‘ και διανυσματικούς κυματαριθμούς k και k‘.

Επιλέγοντας την Ιρλανδία ως παράδειγμα εργασίας, οι κύριες τρεις δυνατότητες δημιουργίας δευτεροβάθμιων μικροσεισμών συνοψίζονται στο Σχήμα 1. Η Κατηγορία Ι (Class I) αντιπροσωπεύει ένα μεγάλο σύστημα καταιγίδας (S1), που δημιουργεί άνεμο και κύματα σε πολλές κατευθύνσεις, συμπεριλαμβανομένων αντιτιθέμενων οδευόντων κυμάτων. Ο μηχανισμός της Κατηγορίας Ι για τη δημιουργία στάσιμων κυμάτων και δευτεροβάθμιων μικροσεισμών έχει ως αποτέλεσμα μιαν περιοχή προέλευσης μικροσεισμών κοντά στο σύστημα καταιγίδας, στο σημείο A. Η Κατηγορία ΙΙ (Class II) περιγράφει τη δημιουργία στάσιμου κύματος μέσω παράκτιας ανάκλασης οδευόντων κυμάτων που δημιουργούνται μακριά από την ακτή (π.χ. S1). Αυτά τα ανακλώμενα κύματα αλληλοεπιδρούν με επακόλουθα προσπίπτοντα κύματα για να δημιουργήσουν στάσιμα κύματα οπουδήποτε μεταξύ της πηγής των προσπιπτόντων κυμάτων και του ανακλαστικού συνόρου, στο σημείο Β. Η κατηγορία III αναφέρεται στη δημιουργία στάσιμων κυμάτων (σημείο Γ) μέσω της αλληλεπίδρασης θαλάσσιων κυμάτων λόγω τοπικών ανέμων, που δημιουργούνται από ένα σύστημα (το S2) και ένα μακρινό φούσκωμα από το S1.

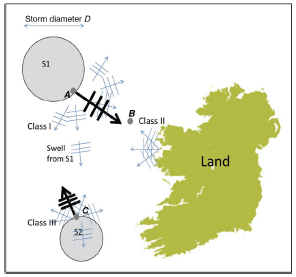
Σχήμα 1. Μηχανισμοί δημιουργίας δευτεροβάθμιων μικροσεισμών στο πεδίο των θαλάσσιων κυμάτων (Πηγή: [1])

Αν και η συμπιεστότητα παίζει ρόλο, εστιάζοντας την προσοχή στις διακυμάνσεις της (δυναμικής) πίεσης στη στήλη ύδατος από την ελεύθερη επιφάνεια ως τον πυθμένα της θάλασσας, μπορεί να υποστηριχθεί με ποσοτικό τρόπο ο θεωρητικός μηχανισμός της δημιουργίας δευτεροβάθμιων μικροσεισμών. Εκτελώντας μια μαθηματική ασυμπτωτική ανάλυση προκύπτει ότι, στη 2^η  τάξη, σε έναν ωκεανό βάθους h, αυτή η αλληλεπίδραση οδηγεί μεταξύ άλλων όρων σε έναν όρο πίεσης συχνότητας f + f ‘και διανυσματικού κυματαριθμού k + k‘. Για σχεδόν αντίθετα διανύσματα k και k‘ με σχεδόν ίσο μήκος, προκύπτει ότι f + f ‘ ∼ 2f και |k + k‘|h ≪ 1. Το πεδίο πίεσης έχει έτσι μιαν πολύ μεγάλη φασική ταχύτητα 2π(f + f ′)/|k + k′| που ταιριάζει με την οριζόντια φασική ταχύτητα ηχητικών κυμάτων στον ωκεανό. Επιπλέον, σε αντίθεση με τους άλλους όρους στο πεδίο της προκαλούμενης από τα κύματα πίεσης που εξασθενούν ταχέως με το βάθος, το πεδίο πίεσης 2^ης τάξης είναι, σε μια δεδομένη στιγμή, ομοιόμορφο μέσα στη στήλη ύδατος εκτός πολύ κοντά στην ελεύθερη επιφάνεια. Παράγει κύματα συμπίεσης 2^ης τάξης στο στρώμα του ύδατος, τα οποία με τη σειρά τους παίζουν ρόλο στη διέγερση (κυρίως) κυμάτων Rayleigh στην επιφάνεια της γης (και στον βυθό της θάλασσας). Εξετάζοντας τη μετατόπιση του πυθμένα της θάλασσας λόγω συγκεντρωμένης δύναμης στην άνω επιφάνεια του ύδατος, αποδεικνύεται ότι το αποτέλεσμα του συντονισμού θα είναι η αύξηση της διαταραχής κατά ένα παράγοντα της τάξης του 5 από την τιμή του σε ρηχά νερά. Για παράδειγμα, μπορεί να συναχθεί το συμπέρασμα ότι η μετατόπιση από μιαν περιοχή καταιγίδας 1000 km² είναι επαρκής να προκαλέσει μικροσεισμούς σε απόσταση 2000 km, υπό την προϋπόθεση ότι υπάρχει παρεμβολή μεταξύ ομάδων κυμάτων της ίδιας συχνότητας που οδεύουν σε αντίθετες κατευθύνσεις. Κατάλληλες συνθήκες κυματικής συμβολής ενδέχεται να παρουσιασθούν στο κέντρο μιας κυκλωνικής κοιλότητας ή αν συμβεί παράκτια ανάκλαση κύματος. Στην τελευταία περίπτωση οι μικροσεισμοί είναι πιθανό να είναι μικρότεροι, εκτός ίσως σε τοπικό επίπεδο.

Οι περίοδοι των μικροσεισμών πρέπει να είναι το ½ αυτών των αντίστοιχων κυμάτων, αν και μπορεί να αναμένεται μια προφανής μετατόπιση στο φάσμα συχνοτήτων λόγω της διακύμανσης της απόκρισης συχνότητας με το βάθος του ωκεανού και της πιο απότομης απόσβεσης των υψηλότερων συχνοτήτων. Η μείωση των διακυμάνσεων της πίεσης με το βάθος είναι εκθετική, σύμφωνα με τη μαθηματική ασυμπτωτική θεωρία 1^ης τάξης. Ωστόσο, όσον αφορά την προσέγγιση της 2^ης τάξης του στάσιμου κύματος υπάρχει μια διακύμανση της πίεσης 2^ης  τάξης που δεν εξασθενεί με το βάθος, και που εν τέλει κυριαρχεί για κάποιες γενικές προϋποθέσεις. Μπορεί να δειχθεί ότι σε μιαν άπειρη αλληλουχία κυμάτων υπάρχει γενικώς μια διακύμανση της πίεσης 2^ης τάξης σε ‘άπειρο’ βάθος (όπου με άπειρο υπονοείται ‘επαρκώς μεγάλο’) που εφαρμόζεται εξίσου σε ολόκληρο το υγρό και δεν συνδέεται με κίνηση σωματιδίων. Στην περίπτωση δυο κυμάτων ίσου μήκους κύματος που οδεύουν σε ακριβώς αντίθετες κατευθύνσεις αυτή η διακύμανση της πίεσης είναι ανάλογη προς το γινόμενο των πλατών 1^ης τάξης των δυο κυμάτων και έχει διπλάσια συχνότητά από αυτά.

Έτσι για την ποσοτικοποίηση της παραπάνω θεωρίας, μπορεί να εφαρμοσθεί μια ασθενώς μη γραμμική ανάλυση (βλέπε [1]) για τις εξισώσεις που διέπουν το πρόβλημα συνοριακών τιμών που περιέχει το σύστημα επιφανειακών κυμάτων στον ωκεανό και τη στήλη ύδατος μέχρι τον πυθμένα της θάλασσας, για να προκύψουν πλήρεις παραστάσεις, όχι μόνο για την πίεση αλλά και για τη μετατόπιση της ελεύθερης επιφάνειας και του δυναμικού ταχύτητας. Με αυτό τον τρόπο μπορεί να υπολογισθεί ο βαθμός εγγύτητας – όσο αφορά στο πλάτος, τη συχνότητα και την προσπίπτουσα γωνία – που απαιτείται για είναι το πεδίο πίεσης 2^ης τάξης επαρκώς μεγάλο. Από τις εγγραφές παράκτιων σεισμικών σταθμών, μπορεί να προσδιορισθούν χαρακτηριστικά κυμάτων, όπως περίοδος και ύψος. Συνεπώς, χρειάζεται να υπάρχει γνώση για την κατάσταση της θάλασσας που επιτρέπει επαρκώς μεγάλες διακυμάνσεις της πίεσης στον βυθό της θάλασσας ικανές να παράγουν μικροσεισμούς, για το πώς αυτές οι διακυμάνσεις της πίεσης μεταβάλλονται στον χώρο και στον χρόνο και πώς αλληλοεπιδρούν με τον πυθμένα. Αποτελέσματα της παραπάνω ανάλυσης για δύο τρισδιάστατα οδεύοντα σε σχεδόν αντίθετες κατευθύνσεις κύματα διαφορετικών διανυσματικών κυματαριθμών k και k‘, πέραν από το στάσιμο κύμα που είναι αποτέλεσμα δυο οδευόντων κυμάτων σε ακριβώς αντίθετες κατευθύνσεις, απεικονίζονται στο Σχήμα 2.

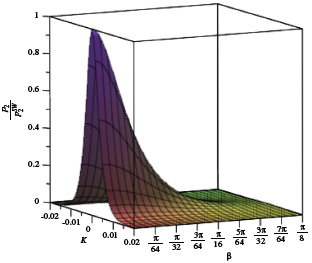
Σχήμα 2. Αδιάστατη πίεση 2^ης τάξης p₂/p₂^SW (p₂^SW είναι η πίεση του στάσιμου κύματος) vs. K = |k| – |k’| και γωνίας μεταξύ των κυμάτων β, για |k| = 0.04 m⁻¹ (περίοδος κύματος T = 10 s) και βάθος h = 400 m.

Άλλες παρατηρήσεις από την παραπάνω ανάλυση μπορεί να συνοψισθούν ως εξής:

(α) Για δυο δισδιάστατα κύματα που οδεύουν σε αντίθετες κατευθύνσεις με τον ίδιο κυματαριθμό, η πίεση 2^ης τάξης είναι ανεξάρτητη από το βάθος, περιοδική ως προς τον χρόνο με διπλάσια συχνότητα από τα κύματα μεταφοράς, και ανάλογη προς τα πλάτη τους.

(β) Για δυο δισδιάστατα κύματα που οδεύουν σε αντίθετες κατευθύνσεις με διαφορετικούς  κυματαριθμούς, η πίεση 2^ης τάξης εξαρτάται από το βάθος, είναι περιοδική ως προς τον χρόνο και τον χώρο και ανάλογη προς τα πλάτη τους.

(γ) Μικρές διακυμάνσεις στους κυματαριθμούς  προκαλούν μεγάλες διακυμάνσεις του πλάτους της πίεσης 2^ης τάξης. Η μέγιστη διαφορά στους κυματαριθμούς για να προκύψουν διακυμάνσεις της πίεσης 2^ης τάξης που να μπορούν να ανιχνευθούν εξαρτάται από την τιμή της περιόδου του κύματος μεταφοράς και ελαττώνεται όταν η περίοδος ελαττώνεται. Αυτό θα μπορούσε να εξηγήσει γιατί οι μικροσεισμοί είναι πολλές φορές τοπικοί στον χώρο και τον χρόνο.

Πηγές:

[1] Pellet, L., Christodoulides, P., Donne, S., Bean, C.J. and Dias, F., 2017. Pressure induced by the interaction of water waves with nearly equal frequencies and nearly opposite directions. Theoretical and Applied Mechanics Letters, 7(3), pp.138-144.

[2] Longuet-Higgins, M.S., 1950. A theory of the origin of microseisms. Phil. Trans. R. Soc. Lond. A, 243(857), pp.1-35.